Section 5.5 Bringing in Calculus
Let
\(p(t)\) represent the position at time
\(t\) of a ball under the influence of gravity. That is,
\(p(t)\) tells us how far the ball has moved from its starting position,
\(p(0)\text{,}\) after
\(t\) seconds. Our goal is to use Galileo’s discovery that
\(g=9.8\frac{\text{meters}}{\text{second}^2}\) to find a formula for
\(p(t)\text{.}\)
During an (infinitesimal) instant of time \(\dx{t}\text{,}\) the velocity is virtually constant so during that instant of time, \(\dx{t}\text{,}\) the infinitesimal change in position, \(\dx{p}\) is given by
\begin{equation*}
\dx{p}=\text{velocity }\times\text{ change in time} =v\dx{t}.
\end{equation*}
But from
equation (5.4) we also know that
\(v=9.8t\text{,}\) so
\(\dx{p}=9.8t\dx{t}\text{.}\)
Thus finding the position of the ball at any time reduces to finding an expression for \(p(t)\) that satisfies the differential equation
\begin{equation}
\dx{p}=9.8t\dx{t}.\tag{5.5}
\end{equation}
Problem 5.5.1.
Since we don’t (yet) have a procedure for solving differential equations like
equation (5.5) we will make an educated guess, and then confirm that our guess works.
From the Power Rule the differential of a quadratic expression like
\(k t^2\) will be the linear term
\(2k
t\dx{t}\text{,}\) so
\(p(t)=k t^2\) seems like a reasonable guess.
(a)
\begin{equation*}
k=4.9=\frac{g}{2}.
\end{equation*}
(b)
Earlier we reasoned that a ball dropped from a height of
\(9.8\) meters would strike the ground between one and two seconds after being dropped. Use
\(p(t)\) to find out exactly how long it takes.
(c)
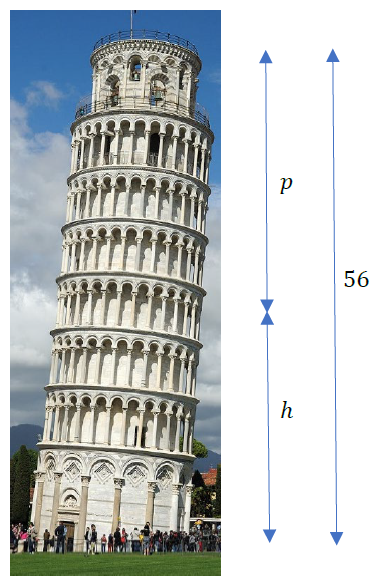
How long would it take the ball to hit the ground if dropped from the top of the Tower of Pisa (a height of
\(56\) meters?
(d)
Evaluate
\(\eval{\dfdx{p}{t}}{p}{56}\text{.}\) What does this represent physically?
Hint.
Remember that
\(\dx{p}\) is a change in position and
\(\dx{t}\) is a change in time.
To summarize the results of
Problem 5.5.1 we see that if
\(p = p(t)=\frac{g}{2}t^2\) denotes the position of a dropped ball at time
\(t\text{,}\) the following statements are true.
-
The velocity of the ball is given by
\(v =\dfdx{p}{t}(=gt)\text{.}\)
-
The rate of change of the velocity (acceleration) is then.
\begin{equation*}
\label{eq:AccelerationAsSecondDerivative}
\dfdx{v}{t}=\dfdx{\left(\dfdx{p}{t}\right)}{t}=g.
\end{equation*}
Notice that in our diagram we also introduced the variable
\(h\) which represents the height of the ball from the ground. The way we choose to define our variables can have a considerable impact on the way we understand a given problem. Here for example both
\(p\) and
\(h\) give us the position of the ball but if
\(p(t)=4.9t^2\text{,}\) then
\(p=0\) represents the top of the tower and the positive direction is down. Conversely, if
\(h(t)=56-4.9t^2\text{,}\) then
\(h=0\) represents ground level and the positive direction is up.
Our examination of Galileo’s work affords us the opportunity to broaden our understanding of the meaning and use of differentials and differential notation. In
Problem 5.5.1 we used
\(p(t)\) to represent the distance that the ball has fallen at time
\(t\text{.}\) In that case it turned out that
\(\dfdx{p}{t}\) represents the velocity with which the ball is falling at time
\(t\text{.}\) This is at once mundane and profound.
It is mundane because velocity has always been defined as distance (
\(\dx{p}\)) divided by elapsed time (
\(\dx{t}\)), and this remains true even when the distance and the time are infinitesimals.
It is profound because the (instantaneous) velocity
\(v(t)\text{,}\) of the ball is always some finite quantity, but we compute it using the quotient of two differentials,
\(\dx{p}\) an
\(\dx{t}\) in this case.
A
differential ratio, for example
\(\dfdx{p}{t}
\text{,}\) is a fundamental concept. In general if some quantity, say
\(y\) is changing in time then
\(\dfdx{y}{t}\) represents the (instantaneous) rate of change of
\(y\text{.}\)
In
Problem 5.5.1 we saw that the velocity of the falling ball is also changing in time, just like its position. Thus we can turn around and compute the instantaneous change in velocity (the acceleration) by computing the differential of the velocity
\(\dx{\left(\dfdx{p}{t}\right)}\text{,}\) and dividing by
\(\dx{t}\text{,}\) giving
\(\dfdx{\left(\dfdx{p}{t}\right)}{t}\text{.}\) This very awkward notation is often abbreviated as
\(\dfdxn{p}{t}{2}\text{.}\) Notice that the acceleration is the result of the following set of computational steps:
-
Differentiate
\(p\text{.}\)
-
Divide by
\(\dx{t}\text{.}\)
-
Differentiate
\(\dfdx{p}{t}\text{.}\)
-
Divide by
\(\dx{t}\) again.
As you become more fluent with these computations you will inevitably begin to combine these steps. Your teacher probably already does. However, the computation of a differential ratio always involves finding the differential of some
finite quantity and then dividing by another differential. If your instructor computes a differential ratio and you don’t see how it was done, ask them to show you each differentiation and division.
If we read the abbreviated notation
\(\dfdxn{p}{t}{2}\) literally it seems to suggest that
\(\dx^2p=\dx(\dx{p})\) is meaningful but the notion of taking the differential of a differential is fraught with logical difficulties. We will begin to address these in
Section 6.8. For now we can avoid pitfalls by recognizing that expressions like
\(\dfdxn{y}{x}{n}\) or
\(\dfdxn{x}{t}{n}\) are the result of differentiating some fininte quantity (
\(y\text{,}\) \(x\text{,}\) \(\dfdx{y}{x}\text{,}\) whatever) and dividing by the differential of the variable (
\(\dx{x}\text{,}\) \(\dx{t}\) whatever)
\(n\) times. We will explore this bit further in the next section.
Problem 5.5.2.
Consider a ball moving vertically so that its height at time \(t\) seconds is given by
\begin{equation*}
h(t) = 56+49t-4.9t^2 \text{ meters.}
\end{equation*}
(a)
Determine the ball’s initial
-
Position.
-
Velocity.
\(\displaystyle \eval{\dfdx{h}{t}}{t}{0}\)
-
Acceleration.
\(\displaystyle \eval{\dfdx{\left(\dfdx{h}{t}\right)}{t}}{t}{0}\)
Remember to go through the two step process of differentiating and then dividing by \(\dx{t}.\) We insist.
(b)
Is “up” the positive or the negative direction?
(c)
How high will the ball go?
(d)
When will the ball hit the ground?
(e)
What is the impact velocity?
(f)
Describe in words the physical situation being modeled by the formula
\(h(t) = 56+49t-4.9t^2 \text{ meters}\text{?}\)
(g)
In general, the height of an object falling near the surface of the earth is given by
\begin{equation*}
h(t)=h_0+v_0t-4.9t^2
\end{equation*}
meters.
-
Show that the initial height is
\(h_0\text{,}\) the initial velocity is
\(v_0\text{,}\) and the acceleration is
\(=-9.8\text{.}\)
-
For simplicity, assume
\(h_0=0\text{.}\) How high will the ball go?
-
Suppose we double our initial velocity. Would the ball go twice as high? Compare this to your guess in
Problem 5.4.2.
Since the graph of
\(h(t)=h_0+v_0t-4.9t^2\) is a parabola it is tempting to conclude that we have shown that an object falling under the influence of gravity alone must be a parabola. But this not correct. We have consistently assumed that the ball is falling vertically so its flight path is a straight vertical line, not a parabola. The graph of
\(h(t)\) is not the flight path of the ball.