An "Easy" Problem From Geometry

Section 2.3 An “Easy” Problem From Geometry

Ideas are like rabbits. You get a couple and learn how to handle them, and pretty soon you have a dozen.
🔗

―John Steinbeck (1902—1968)
🔗

We’ve chosen the following example because it is neither particularly easy nor particularly difficult. It is typical of the kinds of medium level problems that appear in most Calculus textbooks.

🔗

Example 2.3.1.

The lengths of two sides of a triangle are \(a\) and \(b\text{.}\) If the third side is chosen in such a way that the area of the triangle is as large as possible what is the length of the third side?

🔗

You may be able to intuit the correct answer to this problem. That’s OK, but you should try to solve it, too. By “solve” we mean that you should be able to explain to someone with the same mathematical skills you have at the moment why your answer is correct.

🔗

Aside: Comment.

Before reading further do your best to solve this problem. We’ll wait.

🔗

At first it is difficult to see where to begin. (That’s why it’s called a problem.) Don’t let this stop you! In our experience the most common mistake is giving up too soon.

🔗

Don’t. Do. That. Keep thinking.

🔗

Solution. (Partial)

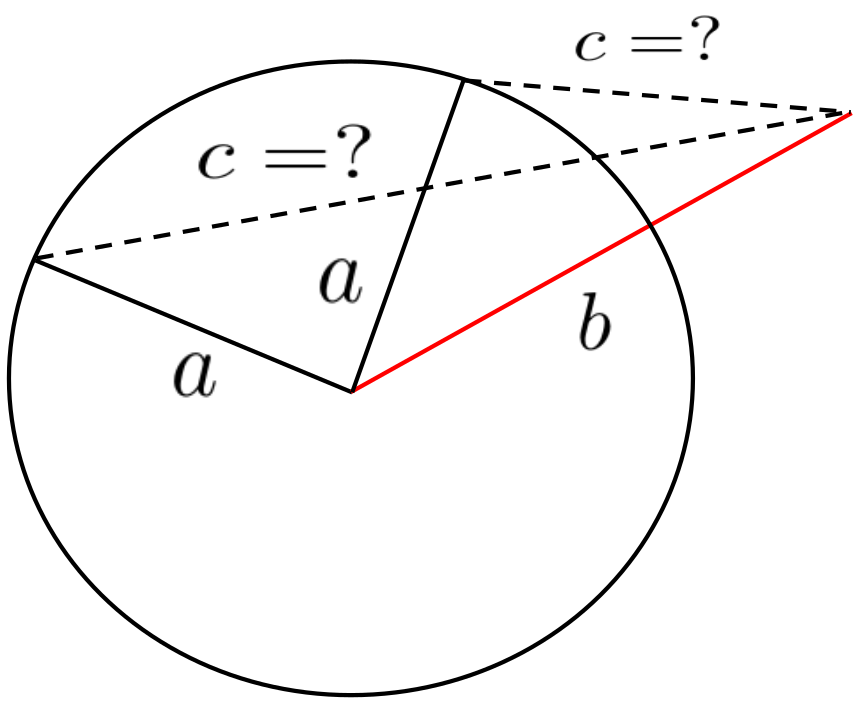
Since we know the lengths of the sides \(a\) and \(b\) of our triangle let’s draw it. The sketch below would be typical. The question is, what length for side \(c\) makes the total area enclosed by the triangle as large as it can possibly be?

🔗

Now what?

🔗

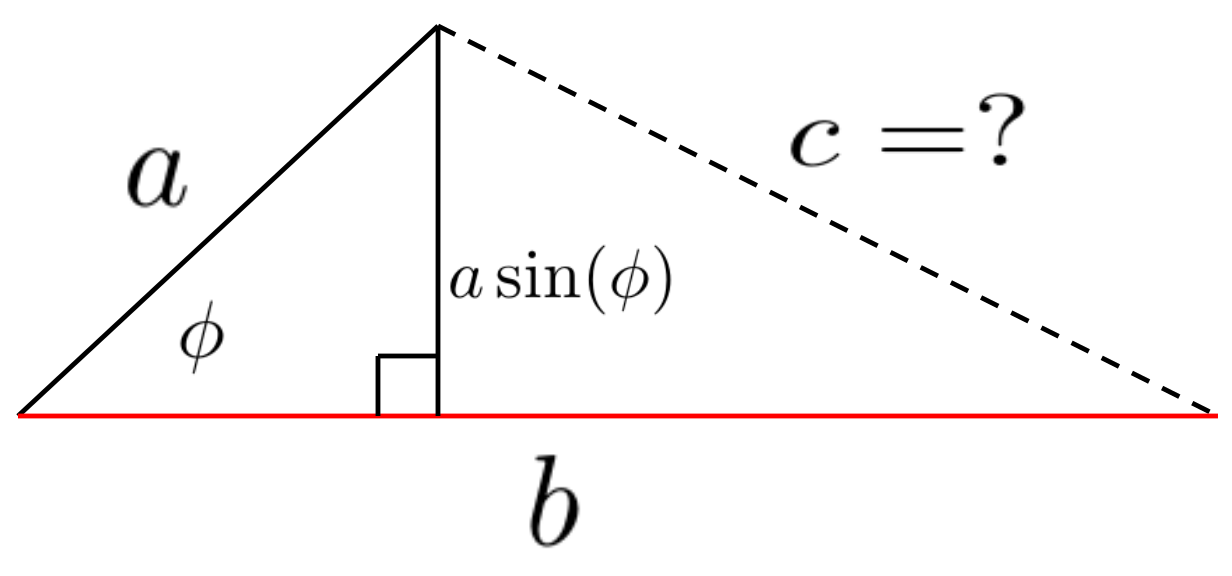
Well, this looks like a right triangle doesn’t it? If it is a right triangle, then we can find the length of \(c\) via the Pythagorean Theorem: \(c=\sqrt{a^2+b^2},\) right?

🔗

Before you go on take a moment and really think about this problem. Can it really be that simple? Can you find any flaws in our reasoning.

🔗

Once you think about it you see that we have no reason to believe that the triangle we seek must be a right triangle. It was completely accidental that we drew our diagram that way. If this seems like a simple-minded mistake, the sort of mistake that you would never make, be careful. It is a mistake to rely too heavily on the diagrams we draw. But it is an easy mistake to make, especially when the problems are more complicated, because as problems get complex we will need to rely on visualization more and more. This was not a dumb mistake. It was just a bit careless, and it is easy to be careless, especially when we first start thinking about a problem.

🔗

DIGRESSION: Making Mistakes.

Being wrong isn’t a bad thing like they teach you in school. It is an opportunity to learn something.
🔗

―Richard Feynman (1918–1988)
🔗

Experience is the name everyone gives to their mistakes.
🔗

―Oscar Wilde (1854—1900)
🔗

Sadly, mistakes are too often seen as a source of embarrassment. Too many students will berate themselves every time they make a mistake. Don’t do that. It is pointless and counter-productive. All it will do is destroy your self confidence. Don’t do it. Learning Calculus can be hard, but you would not have made it this far if you couldn’t do it.

🔗

By definition, mistakes are wrong. A mistake is always obvious after you recognize it as a mistake. Everyone makes mistakes in the course of solving a problem. The process of making mistakes, recognizing them as mistakes, and figuring out why they are mistakes is called learning. The very smartest people, for example Isaac Newton, Gottfried Leibniz, Galileo, Pierre Fermat, Marie Curie, Emmy Nöther, Albert Einstein, or Richard Feynman, made lots of mistakes. Making mistakes is how they got to be smart.

🔗

Isaac Newton was once asked how he had been able to solve problems that no one before him had solved. His reply: “By thinking, and thinking, and thinking about them.” Of course, when he described his solutions he left out all of the errors like anyone would do, because, who cares about those? Making mistakes doesn’t typically get the attention it deserves. An expert is someone who has made every possible mistake. This is why your teacher, an expert, will seldom err. And will be embarrassed when they do.

🔗

Each mistake you make reflects the level of your current understanding of the problem. Each mistake you make takes you a little closer to expertise. Embrace your mistakes and make lots of them! They are proof that you are making progress. But make no mistake (gasp!) about it, making and embracing a mistake is just the first step. You also have to figure out what went wrong.

🔗

So keep making mistakes. Ask for help when you need it. And don’t give up. You have not failed until you stop trying.

🔗

END OF DIGRESSION

🔗

Let’s look at this problem again. The triangle we seek might look like the first one we drew, or it might look like either of the ones drawn in the diagram below, or myriad others. We simply don’t have enough information to decide at this point.

🔗

But from the diagrams we’ve drawn so far we can see that one end of side \(a\) must be pinned to one end of side \(b\) and for each angle between \(a\) and \(b\) we have a different possible triangle. We don’t have to think of both of them as in motion. We can think of one of them, say \(b\text{,}\) as fixed while the other swings around their common endpoint. The circle in our diagram indicates all of the possible positions \(a\text{.}\)

🔗

Do you see how that worked? Our first attempt was simple-minded, but by drawing our first, simple-minded sketch, making a stab at a solution, and figuring out why our simple-minded approach won’t work, we were led to this insight: We can think of \(b\) as static, and we can think of \(a\) as swinging freely while pinned to the end of \(b.\)

🔗

Clearly we need to find the angle between \(a\) and \(b\) —- call it \(\phi\) as in the sketch below —- that maximizes the area of the triangle. But which angle does that?

🔗

Whenever triangles are involved it is a good idea to recall your Trigonometry. After all, that’s what Trigonometry is about, isn’t it? Since we are thinking of \(b\) as fixed, we may as well use it as the base. This makes the height equal to \(a\sin(\phi).\) Also, since we’re trying to maximize the area we should probably write down the area formula: \(A=\frac12\text{(b)ase}\times\text{(h)eight}\text{.}\) Thus the area of the triangle is \(A=\frac{1}{2}ab\sin(\phi)\text{.}\)

🔗

Is it clear that our initial guess was correct? The angle, \(\phi,\) that maximizes the area will be the one whose sine is as large as possible. That would be \(\phi=90^\circ\) so \(c=\sqrt{a^2+b^2}\) provides the maximum area.

🔗

You might be a little uncomfortable with our argument that \(a\sin(\phi)\) is maximized when \(\phi=90^\circ\text{.}\) If so, then for you, this problem is not finished. Possibly we’ve made a mistake. Let’s follow our own advice and see why it is a mistake, if it is.

🔗

Problem 2.3.2.

Replace \(a\sin(\phi)\) with \(h\) in the diagram above. Use the Pythagorean Theorem to reason that if \(\phi\lt{}90^\circ\) then \(h\lt{}a\text{.}\) How does this apply to the problem of maximizing the area of the triangle?

🔗

Until we can demonstrate that \(c=\sqrt{a^2+b^2}\) with a convincing and rigorous argument, this problem is not solved. Instead it is only a conjecture; an educated guess. Our evidence so far is very convincing so it is a very well educated guess, but it is still only a guess.

🔗

Prev Top Next